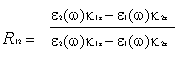|
ROY-GROUP'S CURRENT
RESEARCH PROJECTS:
SECOND HARMONIC GENERATION
(SHG) STUDIES OF METAL-LIQUID INTERFACES
_____________________________________________________
Introduction
Due to their technological importance
and their intriguing but complicated structure, metal-liquid interfaces (MLI)
have secured a special place in the field of surface science. Frequent
applications of MLI are found in various electrochemically controlled surface
processes. However, still a large number of unresolved problems are found in
this area. Here, the interface is electrically charged, populated by polar
and ionic species, and alters both physically and chemically during surface
reactions. The electronic details of such an interface are rather
complicated. At the same time, it is these electronic features of MLI that
play crucial roles in determining the rates and nature of electrode reactions.
The surface second harmonic generation (SHG) work
in our group focuses on these electronic features of surface reactions on
metals.
Traditionally, MLI are
studied with electrochemical methods, including both D.C. (such as voltammetry) and A.C. (such as impedance spectroscopy)
techniques. In both cases, the electrical response of the active interface is
monitored under externally applied voltage modulations. In most cases,
however, these data are overwhelmed by the macroscopic properties of the
surface. Most efforts of the past decade to overcome this problem have
combined electrochemical methods with optical techniques. Linear reflectance
(electroreflectance and differential reflectance)
has become a standard surface tool in this latter category. SHG is a natural
extension of this technique, and provides drastically superior surface
sensitivity compared to linear reflectance (as well as, to the other
traditional methods of linear optics). We are using SHG to investigate variouselectronic properties of MLI. In the following, we
briefly explain how the SHG technique works, and how it allows us to probe
various electronic properties of MLI.
Background: Light Induced
Polarization of an Interface
Let us consider a situation where an electric
field, 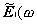 ), at an optical
frequency, w, is incident at an angle, y1, from medium 1 (a liquid in our work) uponmedium 2 (a solid substrate in our
work). The electric field transmitted in medium 2 has the form: ), at an optical
frequency, w, is incident at an angle, y1, from medium 1 (a liquid in our work) uponmedium 2 (a solid substrate in our
work). The electric field transmitted in medium 2 has the form:
(1) 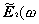 ) = E2(w) e–iwt + complex conjugate, ) = E2(w) e–iwt + complex conjugate,
where E2(w) = E1(w) t12(w), and
t12(w) is the Fresnel coefficient
for transmission from medium 1 to medium 2 . This term depends on the
polarization (and the angle) of the incident light. The angle of refraction
is y2, and the wave
vectors are k1 for medium 1 and k2 for
medium 2. The propagation of the electric field in medium 2 is
confined within a relatively short length, d (skin depth of the substrate material). The intensity, Iw, (power per unit area) of the incident light is
:
(2) Iw = [e1(w)]1/2 |E1(w)
|2/(2p A),
Where A is the area of
illumination, and the dielectric function of medium 1, denoted as e1(w), is considered to be a scalar quantity. In
general, the induced electronic polarization, 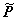 , of the interface has the
form , of the interface has the
form
(3)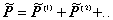 , ,
where the ith
components (i º x,y,z
in a rectangular Cartesian system) of the linear and second order surface
polarization vectors are
(4) 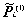 (w) = Pi(1)(w)e –iwt + complex conjugate, (w) = Pi(1)(w)e –iwt + complex conjugate,
(5)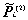 (2w) =
Pi(2)(2w)e –i(2w)t + complex
conjugate, (2w) =
Pi(2)(2w)e –i(2w)t + complex
conjugate,
where
(6) Pi(1)= åj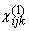 (w) E2;j(w), (w) E2;j(w),
(7) Pi(2)= åj åk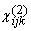 (w,2w) E2;j(w)E2;k(w). (w,2w) E2;j(w)E2;k(w).
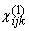 and and 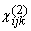 are the first- and second-order
susceptibilities of the solid surface, respectively (the second order
susceptibility of the liquid is zero). The dielectric function, e2;ij(w), of the solid surface is related to are the first- and second-order
susceptibilities of the solid surface, respectively (the second order
susceptibility of the liquid is zero). The dielectric function, e2;ij(w), of the solid surface is related to 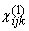 as follows as follows
( 8) e2;ij(w) = dij
+ [4 p 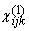 /d], /d],
where dij is
the Kronecker Delta, and d is the thickness of the
surface layer. For small E1(w),
(which is typical of most continuous wave lasers), E2(w) is also small, and then according to Eqs. (6) and (7), |P(2)| <<|P(1)|.
In this case, surface properties are studied by analyzing the behavior of 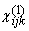 [that is, by analyzing e2;ij(w)]. This is the regime of linear
reflection. For large E1(w) (which is typical of short-pulse
lasers), and depending on the magnitude of [that is, by analyzing e2;ij(w)]. This is the regime of linear
reflection. For large E1(w) (which is typical of short-pulse
lasers), and depending on the magnitude of 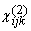 of the surface under study,
|P(2)| can become measurable. This is the regime of nonlinear
(second order) reflection. of the surface under study,
|P(2)| can become measurable. This is the regime of nonlinear
(second order) reflection.
Linear Reflectance of the Interface
In a large number of experiments involving
MLI, the anisotropy in the first order susceptibility of the surface can be
neglected. In these cases,
e2;ij = e2 (a scalar quantity), and
(9) e2
= 1 + [4 pc(1) /d].
For most systems we study, this dielectric function is a
complex quantity, expressed in terms of its real (Re) and imaginary (Im) parts:
(10)
e2 =
Re e2+ Im e2.
The components of the complex wave vectors are related
to e2 as follows
(11)
k1x = k2x = [wn1/c] sin y1
(12)
k1z = [wn1/c]cos y1
(13) k2z = [wn2/c]cos y2.
The real (Re n2) and imaginary (Im n2) parts of the refractive index (n2)
of the solid surface are related toRe e2 and Im e2.
(14) Re e2 = Re n22 – Im
n22
(15) Im e2 = 2 Re n2 Im n2.
The linear reflectance signal has the form, Sw = |R12(w)|2Iw, where R12 is the linear reflection
coefficient,
(16) 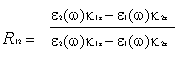
By studying the variations in R12 (at different
frequencies and incidence angles) under different surface conditions, we can
study the surface effects by appropriately analyzing the dielectric
function, e2. In this
technique, however, the optical signal contains some information about the
bulk material of the surface (within the optical skin depth at the
experimental photon frequency).
How Does SHG Work?
The polarization expressed in Eq. (7) is usually considered
with the dipole approximation. In this formulation, 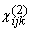 is non-zero only for those
systems where the inversion symmetry is broken. At
the interface, this condition is automatically satisfied. Thus, when an
interface is probed with a high optical field, only the top-most layer of the
surface generates the dipole allowed SH. The oscillating dipoles (a
polarization sheet located in medium 2 immediately below the interface)
radiates at the second harmonic frequency, 2w,
of the incident light [Eq. (7)]. The SHG signal, S2w, has the following form is non-zero only for those
systems where the inversion symmetry is broken. At
the interface, this condition is automatically satisfied. Thus, when an
interface is probed with a high optical field, only the top-most layer of the
surface generates the dipole allowed SH. The oscillating dipoles (a
polarization sheet located in medium 2 immediately below the interface)
radiates at the second harmonic frequency, 2w,
of the incident light [Eq. (7)]. The SHG signal, S2w, has the following form
(17) S2w=
|Fout × P(2)|2,
where Fout
is the output Fresnel factor that contains the dielectric functions
of the interface at the SH frequency, 2w. P(2) is
defined in Eq. (7). Fout depends
on the polarization of the detected SH light. The nonzero elements of 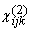 are determined by the symmetry of the surface.
For example, for an isotropic surface, the nonzero and independent elements
of are determined by the symmetry of the surface.
For example, for an isotropic surface, the nonzero and independent elements
of 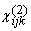 are are 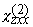 , ,
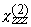 and and 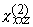 . The result of the dot
product in Eq. (17) depends on the components of P(2) -- which
in turn, are determined by t12 [defined in the context of Eq. (1)]
and hence, by the angle and polarization of the incident light. For
instance, for a p(input)-p(output) combination of polarizations, Eq.
(17) takes the following form . The result of the dot
product in Eq. (17) depends on the components of P(2) -- which
in turn, are determined by t12 [defined in the context of Eq. (1)]
and hence, by the angle and polarization of the incident light. For
instance, for a p(input)-p(output) combination of polarizations, Eq.
(17) takes the following form
(18) S2w(p-p)
= Cp |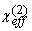 (p-p)|2Iw2, (p-p)|2Iw2,
where Cp is a constant, and 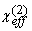 is the effective surface
susceptibility, expressed as is the effective surface
susceptibility, expressed as
(19) 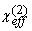 (p-p) = L1p (p-p) = L1p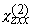 +L2p +L2p 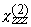 – L3p – L3p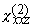 . .
The terms, L1p, L2p and
L3p arise from a combination of Fout
and t12, and contain e1(w),
e1(2w), e2(w) and e2(2w).
Similarly, for
the combination, s(input)-p(output), we have
(20) S2w (s-p) = Cp |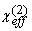 (s-p)|2Iw2, where
Cp is a constant, and (s-p)|2Iw2, where
Cp is a constant, and
(21) 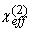 (s-p) = Ls (s-p) = Ls 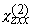 . .
Thus by choosing different combinations of
input and output polarizations, we can probe different components of 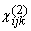 . These different components
of . These different components
of 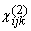 contain
information about different surface features (such as adsorbate
bonds parallel and perpendicular to the interface). In SHG
experiments, we must confirm that the observed signal is indeed SHG, and not
a fluorescence from surface impurities. This is done by verifying (1) the
highly monochromatic nature, and (2) the quadratic power dependence [Eqs. (18) and (20)] of SHG. In a typical experiment, the
intensity (and sometimes, the phase) of the SHG signal from the active
interface is measured as the surface is modified under precise
electrochemical control. Often, the experiments are repeated at different
combinations of the input and output polarizations. The electronic effects on
the surface are manifested in the optical parameters, e2(w), e2(2w), and contain
information about different surface features (such as adsorbate
bonds parallel and perpendicular to the interface). In SHG
experiments, we must confirm that the observed signal is indeed SHG, and not
a fluorescence from surface impurities. This is done by verifying (1) the
highly monochromatic nature, and (2) the quadratic power dependence [Eqs. (18) and (20)] of SHG. In a typical experiment, the
intensity (and sometimes, the phase) of the SHG signal from the active
interface is measured as the surface is modified under precise
electrochemical control. Often, the experiments are repeated at different
combinations of the input and output polarizations. The electronic effects on
the surface are manifested in the optical parameters, e2(w), e2(2w), and
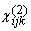 . These parameters control the
observed variations in the phase and intensity of SHG. The SHG data are analyzed to
understand these electronic effects . These parameters control the
observed variations in the phase and intensity of SHG. The SHG data are analyzed to
understand these electronic effects
Some
Important Features of Surface SHG
1)
SHG is intrinsically surface sensitive.
2) It is a non-intrusive tool.
3) It shows fast response to changes in interfacial conditions.
4) SHG is sensitive to both linear and nonlinear optical
properties of the interface.
5) SHG contains information about both structural and electronic properties
of the interface.
6) Both the density and the spatial profile of the interfacial free electron
density can be probed with SHG.
7) Information about crystal induced and image potential surface states can
be obtained through SHG.
8) Electrochemical Stark effects can be probed with SHG.
9) The nature of surface bonds for various adsorbates
can be studied with SHG.
10) Certain effects of surface plasmon resonance
can be measured with SHG.
11) Interband transition in the surface layer, and
its response to changes in surface conditions can be studied using SHG.
SHG Studies in Our Lab
Our
SHG experiments are focused on the
characterization of various metal-liquid interfaces.
Earlier SHG setup in
our lab
Reports of our SHG studies
19. M. J. Walters, C. M. Pettit and D. Roy,
"Surface Kinetics of Eelectrodeposited Silver
on Gold Probed with Potential Step and Optical Second Harmonic Generation
Techniques", Physical Chemistry Chemical Physics 3 (2001) 570-578.
18. D. Roy,
"Comment on Molecular Orientation by Second Harmonic Generation: Self
Assembled Monolayers", Physical Review B
61 (2000) 13283-13286.
17. M.J. Walters, C.M Pettit, F.X. Bock, D.P. Biss
and D. Roy, "Capacitance of a Metal-Liquid Interface During Anion
Adsorption: Phase Selective Measurements in the Presence of D.C. Voltage
Sweep and Finite Solution Resistance", Surface and Interface Analysis
27 (1999) 1027-1036.
16. M.A. Lovell, M.J. Walters and D. Roy,
"Characterization of Electrodeposited Thin Film of Cadmium on Molybdenum
using Optical Second Harmonic Generation", Physical Chemistry
Chemical Physics 1 (1999) 1985-1993.
15. M. J. Walters and D. Roy, "Interference of Linear and Nonlinear
Optical Effects in Second Harmonic Generation from Metal-Liquid Interfaces'',
Applied Spectroscopy 52 (1998) 1554-1568.
14. M. A. Lovell and D. Roy,
"Effects of Sub-Surface Oxygen on Electrodeposition
of Cadmium on Copper'', Electrochimica Acta 43 (1998) 2117-2130.
Addition and Correction 44 (1999) 2327.
13. M. A. Lovell, M. J. Walters and D. Roy,
"Surface Modification of Copper due to Co-Adsorbed Oxygen and Cadmium
Probed with Optical Second Harmonic Generation", Electrochimica
Acta 43 (1998) 2101-2110.
12. M. A. Lovell and D. Roy, "Optical Second Harmonic Generation from
a Catalytically Active Molybdenum Electrode'', Applied Surface Science
135 (1998) 46-52.
11. G. Nagy and D. Roy,
"Optical Second Harmonic Generation as a Probe of Selective Dissolution
of Brass'', Langmuir 11 (1995) 3457-3466. Addition and
Correction, 12 (1996) 1696.
10. G. Nagy and D. Roy,
"Surface Charge Dependence of Second Harmonic Generation from Brass'', Langmuir
11 (1995) 711-715.
9. D. Roy, "DC Field Induced Optical Second Harmonic Generation from
Metal-electrochemical Interfaces'', Electrochimica
Acta 39 (1994) 2699-2703.
Addition and Correction 40 (1995) 2557.
8. R. Gao and D. Roy, "Effects of Diffusion
Limited Mass Transfer on Metal Underpotential
Deposition Voltammograms'', Journal of Applied
Electrochemistry 24 (1994) 1276-1278.
7. G. Nagy and D. Roy,
"Optical Characterization of a Partially Ag-Coated Ni Electrode with
Second Harmonic Generation'', Journal of Physical Chemistry 98
(1994) 6592-6600.
6. G. Nagy and D. Roy,
"Second Harmonic Generation from a Charged Ni Electrode with and without
Anion Adsorption'', Surface Science 320 (1994) 7-16.
5. G. Nagy and D. Roy,
"Surface Charge Dependence of Second Harmonic Generation from a Ni
Electrode'', Chemical Physics Letters 214 (1993) 197-202.
4. G. Nagy and D. Roy, "Oxidation of Cu in Halide Electrolytes
Studied with Optical Second Harmonic Generation'', Langmuir 9
(1993) 1868-1877.
3. R. Gao, T. D. Hewitt and D. Roy, "Stark
Shift of an Interband Transition in Cu Determined
by Surface Charge Measurements'', Journal of Physics and Chemistry of
Solids 54 (1993) 685-690.
2. T. D. Hewitt R. Gao and D. Roy,
"Effects of Surface Charge on the Second Harmonic Generation from a Cu
Electrode'', Surface Science 291 (1993) 233-241.
1. T. D. Hewitt and D. Roy,
"Optical Second Harmonic Generation as a Probe of Hydrogen
Evolution on Copper'', Chemical Physics Letters 181 (1991)
407-412.
|